Eszközallokáció
Ha már tudjuk, hogy pénzünk mekkora hányadát kívánjuk részvényekbe fektetni, már csak azt az apró kérdést érdemes megválaszolni, hogy melyik részvénybe fektessünk. A Markowitz-féle hagyományos hozam-kockázat optimalizációs feladat (Markowitz [1952]) megoldása alapján általánosságban megfogalmazhatjuk, hogy egyedi részvényt nem érdemes vásárolni, hanem csak diverzifikált portfóliót. Tegyük fel, hogy az aktív kezelésben sem hiszünk, ezért meg kívánjuk venni a piaci indexet. No de melyiket, a BUX-ot, vagy valamelyik külföldit? Esetleg azok valamilyen kombinációját?
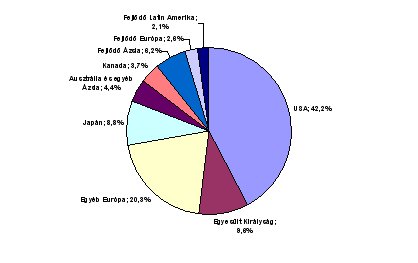
A BUX választása nem tanácsos, ugyanis az lényegében öt részvényből áll, amelyek közül ráadásul kettő azonos ágazatban tevékenykedik, így diverzifikált portfóliónak nem tekinthető. Amennyiben valaki hisz a piacok hatékonyságában, választhatja a CAPM nemzetközi kiterjesztését, az ICAPM-et. Eszerint a piaci szereplők mind optimálisan döntenek, így a globális piaci portfólió hatékony portfólió, azaz úgy tudjuk meg, hogy mi is a számunkra optimális, ha megnézzük, hogy mi az egyes részpiacok kapitalizáció szerinti aránya. Ezt mutatja a következő ábra, amely az MSCI All Countries World index piaci kapitalizáció súlyozású index országsúlyait tartalmazza a 2007. szeptember végi állapot szerint.
3. ábra – Az MSCI All Countries World index megoszlása országok szerint
Eszerint tehát például részvényeink mintegy 40%-át kell az USA piacaira, 10%-át az Egyesült Királyságba, 9%-át Japánba, 20%-át Európába fektetnünk, és így tovább. No de ezzel lemaradunk például a „mindössze” 6,2%-kal szereplő kínai részvények hatalmas szárnyalásáról (vagy éppen összeomlásáról). Mi van, ha mégsem gondoljuk, hogy a globális portfólió optimális is egyben?
A Markowitz-féle hozam-kockázat optimalizációt (amit a Netfolio online portfóliókezelő rendszer is használ) alkalmazhatjuk az egyes eszközosztályokra (részvényindexekre), és így választ kaphatunk arra a kérdésre, hogy ha a jövőben is úgy alakulnának a hozamok, mint a múltban, mi lenne az optimális portfólió, amelyet érdemes tartanunk. Ismert, hogy a részvények hozamának (így a belőlük képzett indexeknek) szórásai illetve kovarianciái autoregresszív folyamatot követnek, így ezek a múlt alapján elég jól előrejelezhetőek. Viszont a hozamokról ez már nem igazán mondható el. Ha ma valaki egy ilyen optimalizációt alkalmaz az elmúlt három évre, akkor azt az eredményt kapja, hogy kínai részvényeket és a kockázatmentes befektetés kombinációját kell tartania. Ennek a megközelítésnek az a fő hátránya, hogy időben igen instabil (erősen függ az eredmény a múltbeli időszak hosszától), másrészt általában nagyon kevés eszközt választ az optimális portfólióba, ellentmondva a diverzifikáció elvének. Vannak kísérletek az optimalizációs eljárás gyakorlati „kikalapálására”: például úgy, hogy a múltbeli hozamok helyett minden eszközre azonos múltbeli átlaghozamot, vagy valamilyen kockázattal korrigált hozamot tesznek a becslésbe. Egy másik irány az, hogy a célfüggvény módosításával érik el, hogy az optimumban a portfólió kellően diverzifikált legyen. Ezekkel a módszerekkel mindössze az a baj, hogy semmilyen elméleti hátterük nincs.
A kétféle megközelítést próbálja ötvözni Black-Litterman [1992] cikke (Black azonos a Black-Scholes modell egyik társszerzőjével). Ebben két alapötlet van. Az egyik az, hogy első lépésben „visszafelé” használják a Markowitz-féle portfólió optimalizációt. Ez azt jelenti, hogy azt határozzák meg, hogy mik lennének azok a várható hozamok, amelyek - és a múltban megfigyelhető szórások és kovarianciák - mellett a globális piaci portfólió optimális lenne. Második lépésben azonban lehetőséget adnak arra, hogy az egyén ezektől az egyensúlyi hozamoktól eltérő várakozásokat állapítson meg, sőt még arra is, hogy valószínűséget adjon annak, hogy az esetek mekkora hányadában fog az egyéni várakozás megvalósulni az egyensúlyi várakozáshoz képest. Például lehet az a várakozásunk, hogy a kínai piacon lufi van, így a piac jövő évi elvárt hozamát -50%-nak gondoljuk az egyensúlyi 15% helyett, de tekintve, hogy egy lufi kipukkadásának idejét nem lehet előre megjósolni, a jövő évben történő kipukkadásnak csak 20% esélyt adunk. A módszert használhatjuk arra is, hogy egy konkrét portfóliót megvizsgáljunk abból a szempontból, hogy milyen hozamvárakozások esetén optimális. Kiderülhet, hogy a gyakorlatban tartott portfóliónk, amelyben 50% a magyar részvények aránya extrémen optimista a magyar piaccal kapcsolatban, így ezt követően eldönthetjük, hogy várakozásunk a helyes, vagy portfóliónk összeállítása helytelen.
Devizaárfolyam-kockázat